在分析各种算法时,经常看到\(O(\log_2n)\)或\(O(n\log_2n)\)这样的渐进复杂度。不知有没有同学困惑过,为什么算法的渐进复杂度中的对数都是以2为底?为什么没有见过\(O(n\log_3n)\)这样的渐进复杂度?本文解释这个问题。
三分式归并排序的时间复杂度
先看一个小例子。
大多数人应该对归并排序(merge sort)很熟悉,它的渐进复杂度为\(O(n\log_2n)\)。那么如果我们将归并排序改为均分成三份而不是两份,其算法时间复杂度是否有变化呢?
递归分析
下面通过递归分析对三分式归并排序的时间复杂度进行分析。因为不管是三分还是二分,对于总共n个数据来说,一遍合并的复杂度为\(O(n)\),所以三分式归并排序的递归式为:
\(T(n)=3T(n/3)+O(n)\)
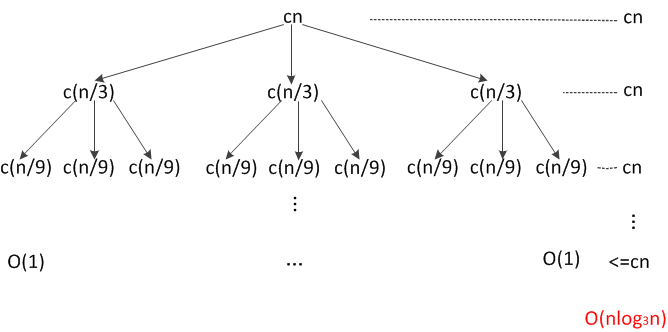
如果把这个递归式的递归树画出来,很容易得到\(T(n)=O(n\log_3n)\)。如下图所示:
对数的陷阱
那么这是否意味着三分式归并排序在时间复杂度上要优于二分式的归并排序呢?因为直觉上\(n\log_3n\)比\(n\log_2n\)要优一些。
实际上三分式归并排序的时间复杂度确实是\(T(n)=O(n\log_3n)\),而且同时也是\(T(n)=O(n\log_2n)\)。
这看起来似乎是矛盾的,\(n\log_3n\)和\(n\log_2n\)当然在绝大多数情况下是不相等的,但是在渐进复杂度情况下就不同了,因为渐进复杂度是忽略常系数的,但是似乎也看不出来\(n\log_3n\)和\(n\log_2n\)是差一个常系数。关键就在于我们应该在中学学过的一个东西:对数换底公式。
\(\log_ab = \frac{\log_cb}{\log_ca}\)
其中a和c均大于0且不等于1。
根据换底公式可以得出:
\(\log_3n = \frac{\log_2n}{\log_23}\)
所以\(n\log_3n\)比\(n\log_2n\)只差一个常系数\(\frac{1}{\log_23}\)。因此,从渐进时间复杂度看,三分式归并并不比二分式归并更优,当然还是有个常系数的差别的。
更一般的:
\(\log_an = \frac{\log_2n}{\log_2a}\)
因此对于大于1的a来说,都与\(O(\log_2n)\)差一个常系数而已,因此为了简便,一般都用\(O(\log_2n)\)表示对数的渐进复杂度,这就解决了本文初始的疑问。当然,以任何大于1的a为底数都是没有问题的。